This post was co-written with David Kurokawa.

In our previous post, we made a case for why explainability is a crucial element to ensuring the quality of your AI/ML model. We also introduced a taxonomy of explanation methods to help compare and contrast different techniques to interpret a model.

In this post, we’ll dive a level deeper and explore the concept of the Shapley value. Many popular explanation techniques — such as QII and SHAP — all make use of Shapley values in their computations. So what is the Shapley value, and why is it central to so many explainability techniques?

What questions do Shapley values answer?

At a high level, the Shapley value approach attempts to explain why an ML model reports the outputs that it does on an input. For example, for a model discerning whether an applicant should receive a mortgage, we might want to know why a retiree Jane specifically has been denied a loan, or why the model believes her chance of defaulting is 70% — this is the query definition.

Implicit in these lines of questioning is why Jane is denied a loan while others are not, or why she’s perceived to have a 70% chance of default while the average applicant receives only a 20% chance from the model. Contextualizing this query with how Jane differs from others helps answer more nuanced questions. For example, when comparing to all accepted applicants, we find the general drivers for her rejection — such as she needs to increase her income substantially. But by comparing her to all fellow retired applicants who were accepted, she might find her above average credit card debt is the critical reason for her predicted high default rate. In this way, Shapley values are contextualized with comparison groups.

The Shapley value approach therefore takes the output of the model on Jane along with some comparison group of applicants, and attributes how much of the difference between Jane and the comparison group are accounted for by each feature. For example, with her 70% predicted default rate and the accepted retiree applicants’ predicted default rate of 10%, there is a 60% difference to explain. Shapley might assign 40% to her credit card debt, 15% to her low net worth, and 5% to her low income in retirement — measuring the average marginal contribution of each feature to the overall score difference. We’ll make this more concrete with a precise formulation of the Shapley value later on.

What are Shapley values?

Shapley values are a concept borrowed from the cooperative game theory literature and date back to the 1950s. In their original form, Shapley values were used to fairly attribute a player’s contribution to the end result of a game. Suppose we have a cooperative game where a set of players each collaborate to create some value. If we can measure the total payoff of the game, Shapley values capture the marginal contribution of each player to the end result. For example, if friends share a single cab to separate locations, the total bill can be split based on the Shapley value.

If we think of our machine learning model as a game in which individual features “cooperate” together to produce an output, which is a model prediction, then we can attribute the prediction to each of the input features. As we will explore later, Shapley values are axiomatically unique in that they satisfy desirable properties to measure the contribution of each feature towards the final outcome.

At a high level, the Shapley value is computed by carefully perturbing input features and seeing how changes to the input features correspond to the final model prediction. The Shapley value of a given feature is then calculated as the average marginal contribution to the overall model score. Shapley values are often computed with respect to a comparison or background group which serves as a “baseline” for the explanation — this disambiguates the question “Why was Jane denied a loan compared to all approved applicants?” from “Why was Jane denied a loan compared to all approved women?”

What’s so great about the Shapley value?

The Shapley value is special in that it is the only value that satisfies a set of powerful axioms that you might desire in an attribution strategy. We won’t cover the proof of this uniqueness in this post, but let’s highlight a few of these axioms:

• Completeness/Efficiency: the sum of the contribution of each player (feature) must add up to the total payoff (model score) minus the average payoff (model score) of the comparison group.
• Dummy: A player that does not contribute to the game must not be attributed any payoff. In the case of an ML model, an input feature that is not used by the model must be assigned a contribution of zero.
• Symmetry: Symmetric players (features) contribute equivalently to the final payoff (model score).
• Monotonicity: If a player (feature) A is consistently contributing more to the payoff (model score) than a player (feature) B, the Shapley value of player (feature) A must reflect this and be higher than that of player (feature) B.
• Linearity: Let’s suppose that the game payoff (model score) was determined based on the sum of two intermediate values, each of which are derived from the input features. Then, the contribution allocated to each player (feature) must be the sum of the contributions of the player (feature) towards the intermediate values.

How are Shapley values used in the context of ML models?

We mentioned that Shapley values calculate the average marginal contribution of a feature 𝒙 towards a model score. How is this computed in practice?

Let’s first try to formulate this for a cooperative game. Suppose that we have an n-player game with players 1, 2, …, n and some value function v that takes in a subset of the players and returns the real-valued payoff of the game if only those players participated. Then formally, the contribution Φ of player i is defined as

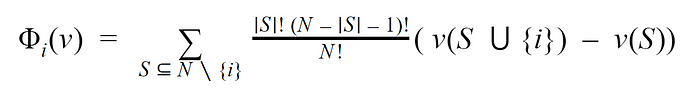
where S is a coalition, or subset, of players. In plain English, the Shapley value is calculated by computing a weighted average payoff gain that player i provides when included in all coalitions that exclude i.

In the simplest ML setting, the players of this cooperative game are replaced by the features of the ML model and the payoff by the model output itself. Let’s return to our mortgage lending example from before to make this clearer. Suppose we have a model that is trained to predict an individual’s chance of defaulting on a loan. Jane receives a 70% chance of defaulting, and we want to understand how important her income (which happens to be feature i) was in determining the model’s decision. We first would pick a random subset of features S to provide to the model. For example, Scould include Jane’s credit card debt and net worth. We would then measure the marginal contribution v(S ∪ {i})-v(S) which tells us how much the inclusion of Jane’s income to the model (feature i) changes the model’s output relative to the model’s output with credit card debt and net worth as the only features. In other words, the marginal contribution captures the incremental contribution of income to the model’s output while accounting for its interaction with the credit card debt and net worth features. The Shapley value is the weighted average of all such marginal contributions over varying S.

For ML models, it’s not possible to just “exclude” a feature when determining a prediction. Thus, the formulation of Shapley values within an ML context simulates “excluded” features by sampling the empirical distribution of the feature’s values and averaging over multiple samples. This can be tricky and computationally expensive depending on the sampling strategy, which is why most real-world methods to compute Shapley values for ML models are producing estimates of the true Shapley value. The core differences between these algorithms, such as QII and SHAP, lie in the nuanced ways that each chooses to intervene upon and perturb features.

Computing Shapley values only necessitates black-box access to the model as a predictor — so long as you know its inputs and outputs, the Shapley value can be computed without any knowledge of the model’s internal mechanics. This makes it a model-agnostic technique, and also facilitates direct comparison of Shapley values for input features across different model types.

In addition, because Shapley values can be computed with respect to an individual data point, they provide the granularity of local explanations while simultaneously allowing for extrapolation. By analyzing which features have higher Shapley values across multiple data points, for example, this can give insight into the model’s global reasoning.

Limitations of Shapley Values

Despite their axiomatic motivation, there are some notable limitations of Shapley values and their use in ML settings.

Computing Shapley values requires selection of coalitions or subsets of features, which scales exponentially in the number of features. This is abated by using approximation techniques and taking advantage of specific model structures when known (such as in tree or linear models), but in general the Shapley value computation is intractable to compute exactly.

A more conceptual issue is that the Shapley value can heavily rely on how the model acts on unrealistic inputs. For example, a housing price model that takes in latitude and longitude as separate features may be queried on real estate in the middle of a lake. There are formulations of the definition that attempt to remedy this, but they suffer from other problems — often a requirement for unattainable amounts of data. This “unrealistic input” problem has even been shown to be exploitable by attackers in that models can be constructed that perform nearly identically to an original model, but whose Shapley values are nearly random.

Shapley Values: A Powerful Explanation Tool

Shapley values borrow insights from cooperative game theory and provide an axiomatic way of approaching machine learning explanations. It is one of the few explanation techniques that are backed in intuitive notions of what a good explanation looks like, it allows for both local and global reasoning, and it is agnostic to model type. As a result, many popular explanation techniques make use of the Shapley value to interpret ML models. In this blog post, we outlined the theoretical intuition behind the Shapley value and why it’s so powerful for ML explainability.

This blog has been republished by AIIA. To view the original article, please click HERE.