In classification a central problem is how to effectively learn from discrete data formats (categorical or ordinal features). Most datasets present us with this problem so I guess it is fair to say that almost all data scientists have faced this at some point (right?).
Despite the existence of different techniques that may mitigate it, this is an issue that involves compromises to get past. A choice is left to the Data Scientist and, aware or not, a poor one can negatively impact results.
The Gumbel-Softmax is a very interesting activation layer that was recently introduced and can help us do just that. I wrote this article to demonstrate the problem it is trying to solve, walk you through the core ideas of the Gumbel-Softmax and help you implement it in your own pipelines with open-source code. As the title suggests we will take a data synthesis approach, and we will try it on GANs.
Let’s get started!
A quick recap on categorical feature synthesis
Synthetic data is becoming a hot topic in an increasingly data-centric AI community. If this topic has caught your attention at some point, then likely you have also heard about Generative Adversarial Networks that got introduced less than 10 years ago but since then came a long way in terms of output quality and range of applications. In fact there are tons of examples of realistic synthetic data generation across a wide variety of tasks such as:
Tabular data synthesis is another interesting application, more ubiquitous and intimately related to the focus of this article, categorical data.
Before training a synthesizer we may preprocess our features. In the case of categorical features, one-hot encodings are used in order to transform discrete features into sparse blocks of 1’s and 0’s. Converting symbolic inputs like categorical features to sparse arrays allows neural network (NN) models to handle the data similarly to very different feature formats like numerical continuous features.
An example:


GAN generators attempt to synthesize sparse categorical inputs from real data. However just like Multi-Layer Perceptrons, when predicting without proper activation functions, the frequent output are logits, i.e. non-normalized probability distributions that can look something like this:

Well look at that. Messy, and in this case we were looking for binary outputs, weren’t we? Producing usable records requires us to infer sensible feature values: we would have to sample the logits somehow (p.e. use the class with highest activation); also this looks like a potential flag for a GAN discriminator to identify fake samples. I’ll admit I am not sure if the last point is that simple but if the the discriminator were able to differentiate real from synthetic samples just based on how they look like (float vectors instead of one-hot vectors) then it would act as a perfect discriminator. A perfect discriminator would make the generator update its parameters based on infinite minimax loss (see from the equation what would happen if the Discriminators estimate is 1 for a real sample and 0 for a fake sample). Expected result? Generator train convergence impossible!
Activation functions like Softmax and Gumbel-Softmax allow us to convert logits output to categorical distributions that can be readily sampled. This is what a Softmax output of the above example would look like:

Now let’s check out in more detail what Softmax and Gumbel-Softmax are and what they can do for the categorical features of our synthetic samples!
Softmax and the Gumbel-Softmax activation
Softmax is a differentiable family of functions. As we saw, they map an array of logits to categorical distributions, i.e. arrays with values bounded in the [0, 1] range and that sum to 1. However these samples can’t help us in gradient descent model learning because they are obtained from a random process (no relation with the model’s parameters). The operations carried out by our generator need to be differentiable and deterministic for us to be able to flow the gradients from one end to the other.
The Gumbel-Softmax (GS) is a special kind of Softmax function that got introduced in 2016 (fun fact: coincidentally it was proposed in the same time by two independent teams) [1], [2]. It works like a continuous approximation of Softmax. Instead of using logits directly Gumbel distribution noise is added before the Softmax operation so that samples from the generator become a combination from a deterministic component, parameterized by the mean and the variance of the categorical distribution, and a stochastic component, the Gumbel noise, which is helping us sample without adding bias to the process.
A temperature parameter, usually called tau or lambda and defined in ]0, inf[ works as a knob to define the base of the exponentiation operation of Softmax. This parameter is usually kept close to 0. Higher bases approximate the uniform distribution, bases close to 0 approximate the true categorical distribution.
The image below shows three different flows attempting to do the same thing, retrieving categorical samples and computing a loss differentiable in all model parameters.
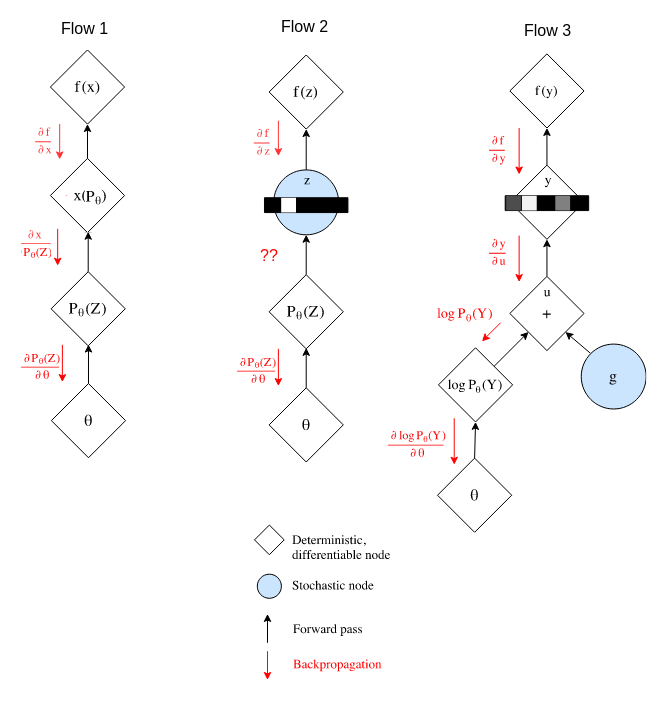
In Flow 1 we use an operation like a soft version of argmax in x to retrieve a one-hot sample (basic argmax is not differentiable). Back propagation will work just fine, the operations in red allow the gradient to flow from the sample loss to the generator parameters. The inconvenient part is that argmax is a winner takes all function. The most likely category gets sampled and there is a significant chance that our synthetic samples will never include minority classes. Boo!
In Flow 2 we do not find the winner takes all behavior, we can actually get realistic samples according to our true categorical distribution. Great! Right? Unfortunately no, the stochastic nature of the sampling process will not allow the gradient to flow back to our model’s parameters, which means no learning. There are alternative strategies such as the Straight-Through that solve this by assuming a constant gradient for the sampling operation. This will allow gradient flow but it will be biased. [2] has more information on this estimator.
Flow 3 is the Gumbel-Softmax, maybe you have heard about the Reparameterization Trick. Here we can see it applied to great effect! The key is the ratio of logits and Gumbel noise scales adjusted by changing the logits scale while the Gumbel noise scale is kept constant. Based in the confidence on its own logits, the model will favor a uniform distribution (lowering the ratio) or its prediction of the categorical distribution (increasing the ratio). Since node y is still not a one-hot encoded vector, we can solve this by making two computations. We use y to complete our gradient computation graph at train time and retrieve a categorical sample from it on prediction time. The discriminator will operate on this one-hot sample but the gradient will flow through the y operation.
Now that we have seen the theory behind the Gumbel-Softmax activation, let’s move to the practical part, categorical data synthetization!
Synthesized categorical features comparison
For the generation of synthetic data we will use the YData Synthetic package. In a recent update the Gumbel-Softmax activation was introduced in all regular data synthesizers. Here is a snippet with the base Gumbel-Softmax layer implementation:

Here we use two versions of the Wasserstein GAN with Gradient Penalty implementation [3]. The standard version that includes the Gumbel-Softmax and an overridden version that does not use it. Both versions are essentially the same, you can see in the following snippet:
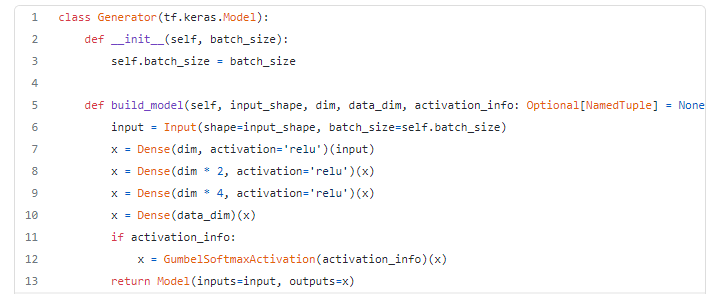
A simple override of the base synthesizer removes the passing of the activation_info argument in so that we can have a generator without Gumbel-Softmax activation. That is the without Gumbel-Softmax generator never executes line 12.
The synthesizers were trained with the adult dataset, below you can see some generator sample outputs for the workclass feature (I chose one feature only because the full samples have 120 columns):


Now let’s look at statistical distributions of original samples, with and without GS implementations:

I hope at this point you can reach some conclusions about the results on top. In any case, here are mine:
- None of the synthetic samples managed to capture the categorical distributions very well. But, to be fair, the model or the training conditions were not optimized for this scenario, I am sure these changes could go a long way.
- The synthesizer with Gumbel-Softmax produced almost uniform samples.
- The synthesizer without Gumbel-Softmax produced samples close to winner takes all behavior.
Wrapping up
We concluded some key points that are aligned with the expectations grounded in the Gumbel-Softmax and categorical features synthesis theory that we walked through.
You are more than invited to play around with the example notebook I used to produce the results, you can find it here! Also feel free to clone or fork the project and play around with the source code if you want to try enhancing the original samples. Tuning the parameter tau of the Gumbel-Softmax activation per example can help us approximate the real categorical distribution.
On a last note, if you’d like to join a group of synthetic data enthusiasts, discuss papers, datasets, models or tackle some issues that you find on the way you are also invited to checkout the Synthetic Data Community. Me and my colleagues will be happy to see you there!
This is my first article in Towards Data Science, thank you for reading it, I hope you have found it useful, and that you managed to learn something new.
References:
[1] C. J. Maddison, A. Mnih and Y. W. Teh, The Concrete Distribution: A Continuous Relaxation of Discrete Random Variables (2016), arXiv
[2] E. Jang, S. Gu, B. Poole, Categorical Reparameterization with Gumbel-Softmax (2016), arXiv
[3] I. Gulrajani, F. Ahmed, M. Arjovsky, V. Dumoulin, A. Courville, Improved Training of Wasserstein GANs (2017), arXiv
This blog has been republished by AIIA. To view the original article, please click HERE.


Recent Comments